Introdução à Ciência de Dados

k-means

Prof. Jodavid Ferreira

UFPE

Aprendizado Não Supervisionado


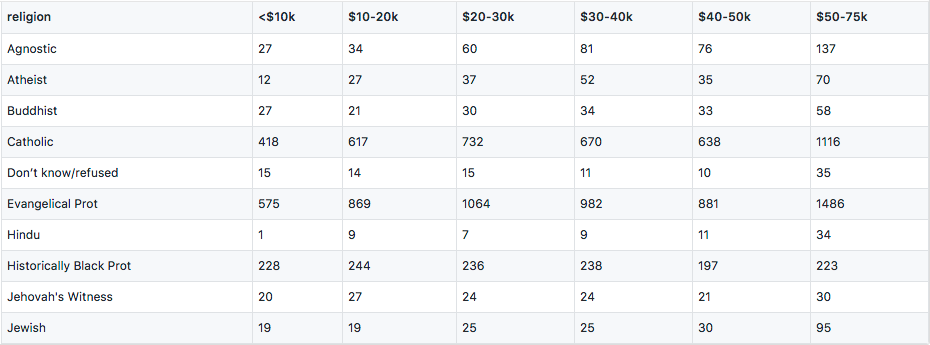
  • De maneira distinta do Aprendizado Supervisionado, os algoritmos de Aprendizado Não-Supervisionado treinam com dados sem rótulos pré-definidos, identificando padrões intrínsecos sem a necessidade de supervisão externa.
  • Alguns tipos de problema que utilizam este tipo de aprendizado são: Clusterização, Redução de Dimensionalidade.

Métodos de Agrupamento


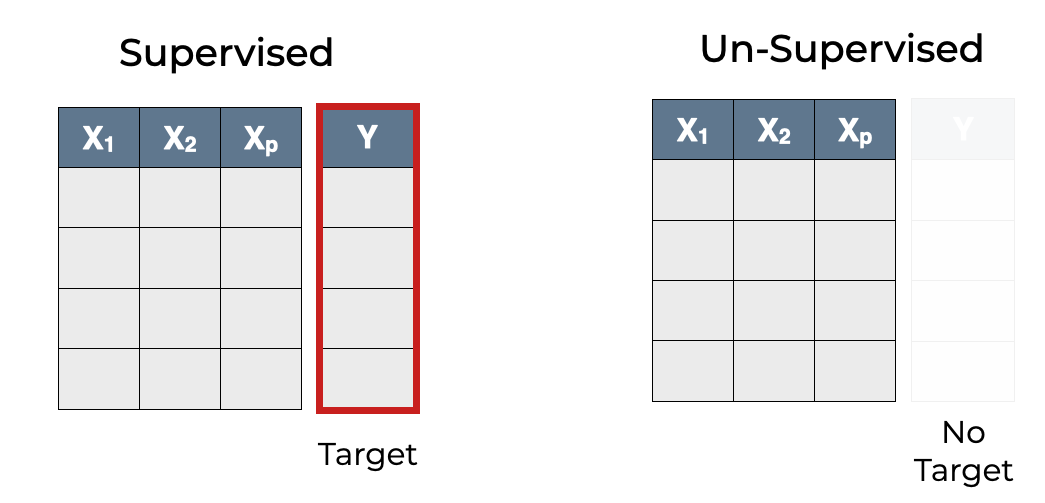
Um paralelo entre os dois modelos de aprendizado pode ser feito com Classificação (Aprendizado Supervisionado) e Clusterização (Aprendizado Não-Supervisionado):

  • Enquanto os algoritmos do primeiro grupo aprendem com exemplos rotulados

  • O segundo busca agrupar dados com características similares sem qualquer indicação prévia de grupos ou categorias;

Métodos de Agrupamento


  • Esta abordagem faz sentido em cenários em que os rótulos dos dados são desconhecidos ou difíceis de obter, como, por exemplo:


    • Nos algoritmos de recomendação do seu aplicativo de Streaming favorito.
      • Ao agrupar telespectadores com gostos semelhantes, as recomendações de novos Filmes/Séries se tornam mais relevantes.

    • Um outro exemplo é a segmentação de clientes, que pode ser utilizada para direcionar campanhas de marketing, ou para entender melhor o comportamento dos consumidores.

Métodos de Agrupamento


De forma geral, é possível dizer que a qualidade de um algoritmo de Clusterização (Agrupamento) é medida de acordo com 2 aspectos:


  • Distância intra-cluster - no agrupamento, quanto menor a distância entre os pontos de um mesmo cluster é melhor;
  • Distância intercluster - quanto maior a distância entre as bordas de 2 clusters distintos também é melhor;

Então, espera-se ter uma menor distância intra-cluster e uma maior distância intercluster.



k-means

Algoritmo k-means


  • O algoritmo K-means é um dos mais conhecidos métodos de Clusterização.

Seja \(\mathbf{X}\) uma matriz de dados, ou base de dados conhecida, com \(n\) linhas e \(p\) colunas,

\[\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^\top = \begin{bmatrix} x_{11} & \cdots & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix}\]

e assuma que um valor \(k\) é dado como número de grupos.

  • O objetivo do algoritmo \(k\)-means é agregar os pontos em \(k\) grupos, de tal modo que a soma dos quadrados das distâncias dos pontos aos centros dos agrupamentos (clusters) seja minimizada. VAMOS ENTENDER ISSO…

Algoritmo k-means


  • O \(k\)-means é um método baseado em centroides, em que tais centroides são os pontos médios de cada grupo;

  • o método busca encontrar \(k\) vetores de pontos, \(\mathbf{c}_1, \ldots, \mathbf{c}_k\) que são os centroides;

  • Usualmente, o valor de \(k\) é conhecido e deve ser fornecido pelo usuário mas é possı́vel obtê-lo por tentativa e erro.

Considere novamente a matriz como sendo nossa matriz de dados:

\[\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^\top = \begin{bmatrix} x_{11} & \cdots & x_{1p} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{np} \end{bmatrix}\]

Algoritmo k-means

Os centroides são encontrados minimizando a soma das distâncias quadradas entre os pontos de cada grupo e o centroide do grupo, chamado de soma das distâncias quadradas intra-clusters (WSS - total within-cluster sum of squares), através da equação:

\[\text{WSS} = \sum_{j=1}^{k} W(g_j),\]

em que, para cada \(g_j\) com \(j \in \{1, \ldots, k\}\), temos:

\[W(g_j) = \sum_{i=1}^{n_j} ||\mathbf{x}_i - \mathbf{c}_j||^2 = \sum_{i=1}^{n_j} \sum_{l=1}^{p} (x_{il} - c_{jl})^2,\] sendo \(||\mathbf{x}_i - \mathbf{c}_j||^2\) é a distância euclidiana, \(\mathbf{x}_i\) é o vetor de pontos, \(\mathbf{c}_j\) o centroide do grupo \(j\) e \(n_j\) é a quantidade de observações em \(g_j\) (no grupo \(j\)).

Algoritmo k-means


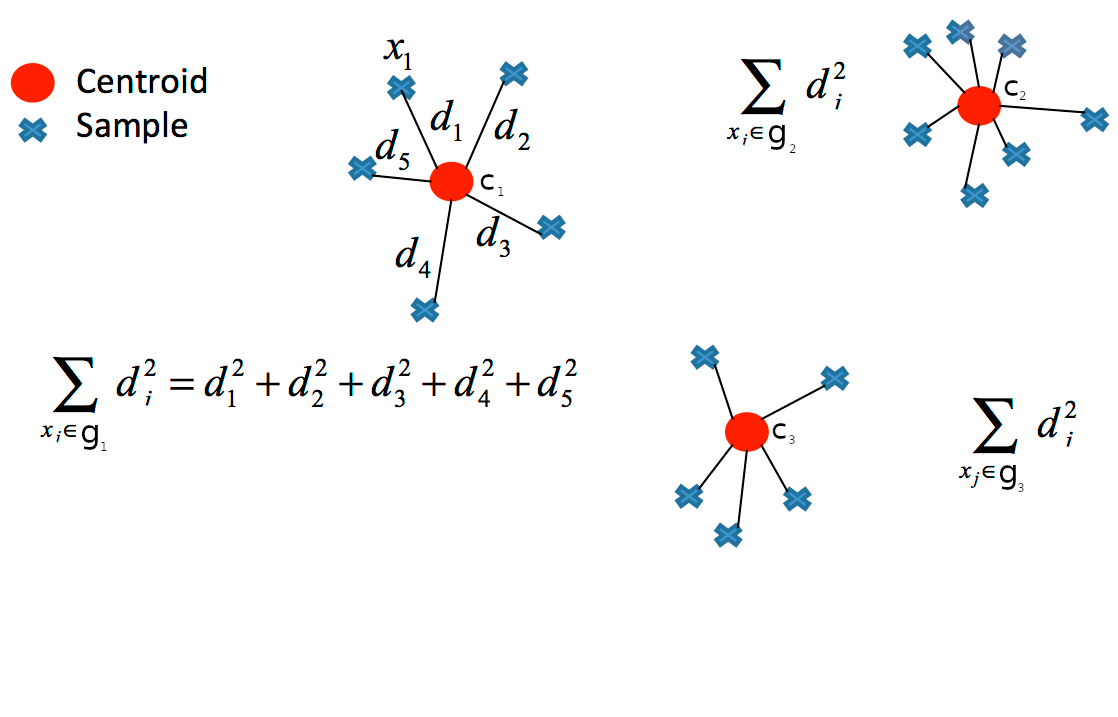
em que, \(d_i^2 = ||\mathbf{x}_i - \mathbf{c}_j||^2\) é a distância euclidiana entre o ponto \(\mathbf{x}_i\) e o centroide \(\mathbf{c}_j\).

Algoritmo k-means



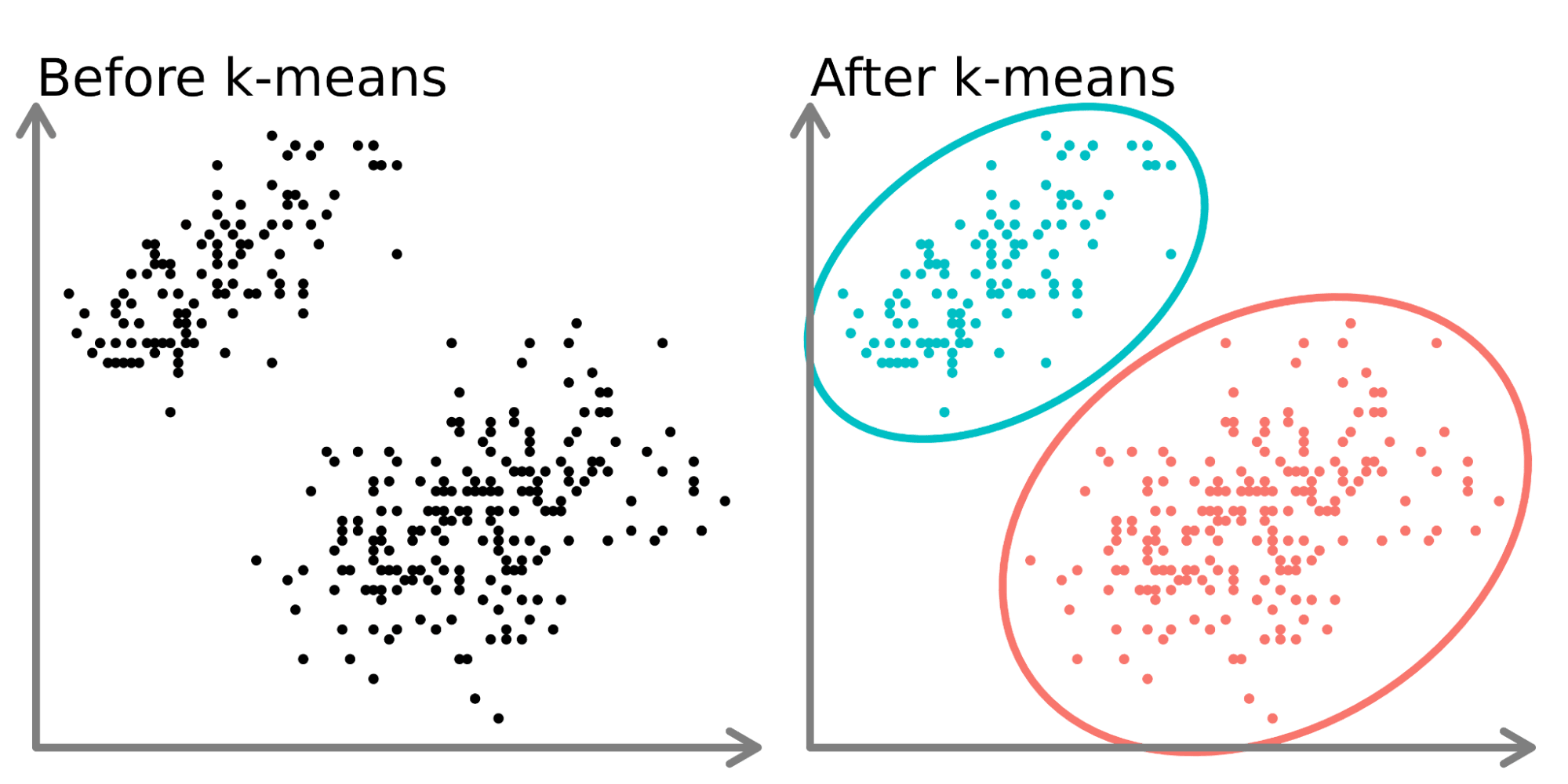
Nesse caso foi realizado um agrupamento \(k\)-means com número de grupos igual a 2.

Algoritmo k-means


Vamos considerar esse exemplo com 100 observações, 3 variáveis, abaixo um exemplo de 5 linhas:

            x          y           z
1 -0.56047565 -0.7152422  1.07401226
2 -0.23017749 -0.7526890 -0.02734697
3  1.55870831 -0.9385387 -0.03333034
4  0.07050839 -1.0525133 -1.51606762
5  0.12928774 -0.4371595  0.79038534

Algoritmo k-means


Algoritmo k-means


Algoritmo k-means

Algoritmo k-means


Temos que o algoritmo consiste nos seguintes passos:

  1. O objetivo é dividir um conjunto de dados em grupos (clusters) semelhantes entre si;

  2. O primeiro passo do processo é selecionar o número de clusters que serão criados, então é determinado um valor para \(k\) e selecionado \(k\) pontos aleatórios do conjunto de dados para serem os centros dos clusters iniciais (Isso deve ser feito com base em algum conhecimento prévio do conjunto de dados, ou a partir de algumas técnicas estatísticas que encontram um valor ótimo);

  3. Associe cada ponto ao centróide mais próximo com base na distância euclidiana;

Algoritmo k-means


  1. Calcule a soma soma das distâncias quadradas entre os pontos de cada grupo e o centroide do grupo, ou seja, encontre o valor de \(W(g_j)\) para cada grupo \(g_j\), com \(j \in \{1, \ldots, k\}\);

  2. Encontre a soma total de quadrados intra-cluster, através da equação:

\[\text{WSS} = \sum_{j=1}^{k} W(g_j) = \sum_{j=1}^{k} \sum_{i=1}^{n_j} ||\mathbf{x}_i - \mathbf{c}_j||^2;\]

Algoritmo k-means


  1. Repita os passos 3, 4 e 5 até que não haja mais mudanças significativas nos centróides dos clusters, sinalizando a estabilidade do algoritmo. Essa estabilidade pode ser verificada através da comparação da soma total de quadrados intra-cluster entre duas iterações consecutivas, ou seja,

\[\left|\text{WSS}^{(t)} - \text{WSS}^{(t-1)} \right| < \varepsilon,\] ou seja,

\[ \left| \sum_{j=1}^{k} W(g_j)^{(t)} - \sum_{j=1}^{k} W(g_j)^{(t-1)} \right| < \varepsilon,\]

em que \(\varepsilon\) é um valor maior que 0 e \(t\) é a iteração.



Vamos ao R e Python

Referências para serem utilizadas


  • Estatística e ciência de dados., Morettin, Pedro Alberto, and Júlio da Motta Singer, 2022.

  • An Introduction to Statistical Learning: With Applications in R, James, G., Witten, D., Hastie, T. and Tibshirani, R., Springer-Verlag, 2013.

  • Aprendizado de máquina: uma abordagem estatística, Izbicki, R. and Santos, T. M., 2020.

Extras:

https://www.sharpsightlabs.com/wp-content/uploads/2021/04/supervised-vs-unsupervised-learning_FEATURED-IMAGE.png



OBRIGADO!

Slide produzido com quarto